Figure: Plot of the OR function and the learned perceptron boundary
The long awaited moment has finally arrived. We are now going to look at the most basic building block of neural networks, the perceptron. The perceptron on its own is just a binary linear classifier. It was orignally proposed by Frank Rosenblatt in 1958. In this model we have an input vector of \(x=(x_{1},...,x_{n})\), weights \(w=(w_{1},...,w_{n})\) and bias \(b\). In this model we classify by inputing into a sign function the inner product of the weights and input vector and adding the bias:
To train the model and learn the weights we can update our weights and bias via subgradient descent:
Here \(\eta\) is our learning rate, \(X^{T}\) is our data matrix and \(e\) is our error vector (\(e_{i}=y_{i,\text{true}}-y_{i,\text{prediction}}\)). Implementing this into code we get:
class Perceptron:
def __init__(self, learning_rate=0.1, n_iters=10):
self.lr = learning_rate
self.n_iters = n_iters
self.weights = None
self.bias = None
def fit(self, X, y):
n_samples, n_features = X.shape
self.weights = np.zeros(n_features)
self.bias = 0
y_ = np.where(y == 0, -1, 1)
for _ in range(self.n_iters):
# Compute predictions for all samples
linear_output = X @ self.weights + self.bias
predictions = np.sign(linear_output)
# Handle sign(0) = 1 (to stay consistent)
predictions[predictions == 0] = 1
# Find misclassified samples
misclassified = y_ * predictions <= 0
# Apply updates using only misclassified samples
if np.any(misclassified):
X_mis = X[misclassified]
y_mis = y_[misclassified].reshape(-1, 1)
# Update weights and bias
self.weights += self.lr * np.sum(X_mis * y_mis, axis=0)
self.bias += self.lr * np.sum(y_mis)
def predict(self, X):
linear_output = np.dot(X, self.weights) + self.bias
return np.where(linear_output >= 0, 1, 0)
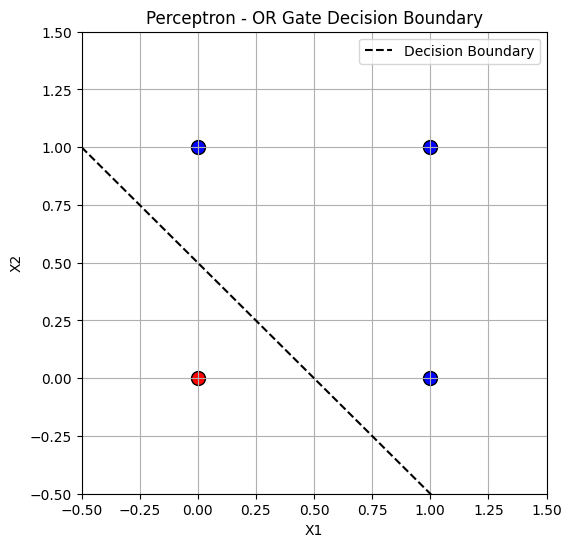
Training it on the OR logic function we get:
We can also train this on any other linearly seperable data and can extend it to non-linearly seperable data using the kernel trick covered in the SVM tutorial.